При выполнении задания ЕГЭ-18 надо:

-знать основные законы алгебры логики;

-уметь выполнять преобразования логических выражений.

Если логическое выражение содержит импликацию, надо избавиться от неё, заменив на комбинацию отрицания и дизъюнкции.

Пример задания ЕГЭ-18

Решение

Преобразуем логическое выражение, избавимся от импликации, заменив выражение А → В на равносильное (¬А) \/ В. Получим:

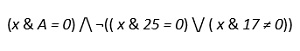
Продолжим преобразование логического выражения, используем равносильность выражений ¬(А \/ В) и (¬А) /\ (¬В). Получим:

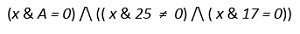
Выражение тождественно ложно, если хотя бы один из трёх множителей равен 0. Если 0 будет равен второй множитель ( x & 25 ≠ 0) или третий множитель ( x & 17 = 0), то от A значение логического выражения не зависит. Поэтому, будем считать, что значения второго и третьего множителей равны 1. Получим:

(x & A = 0) = 0

( x & 25 ≠ 0) =1

( x & 17 = 0) = 1

Переведём числа 25 и 17 в двоичную систему счисления:

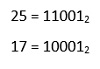
Выпишем второе и третье логические выражения:

Объединим условия:

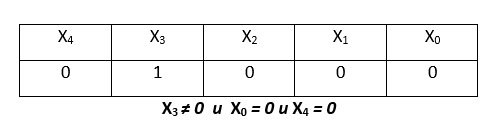
Переведём полученное значение в десятичную систему счисления:

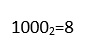
Ответ: 8